Introduction

Les distances de trajet sont une problématique actuelle. De nos jours, des plans sectoriels sont créés pour minimiser les déplacements et favoriser les interactions entre les différents constituants d'une ville.

Objectifs et hypothèses

A travers un modèle viable, nous voulons analyser les organisations spatiales entre différents composants structurels d'une ville. Cette analyse devra permettre de mieux comprendre les interactions entre différents paramètres au sein d'une ville en fonction de leur éloignement respectif.

Nous pensons qu'avec quelques composants types et diverses exigences, nous pouvons recréer des cas analogues à des structures actuelles.

Méthodes et procédures

Premier pas

Pour ce faire, nous avons définis des unités représentant des éléments structurels types d'une ville. Ainsi, une cellule rouge représente une unité d'habitation type, une cellule jaune, une unité d'activité et une cellule inactive, le vide actif.

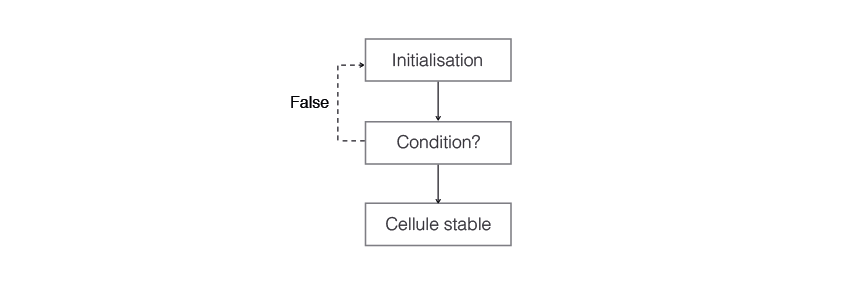
Nous avons émis la condition qu'une cellule d'habitation doit avoir dans un rayon donné r un nombre d'activités X pour être stable. Si la condition n'est pas satisfaite, le processus est réitéré jusqu'à ce que la condition soit satisfaite.

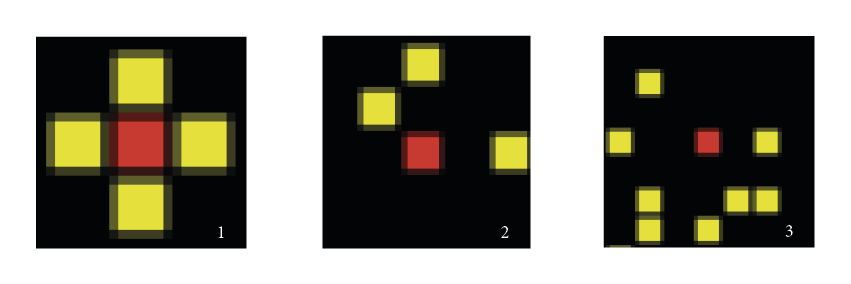
Divers inputs et sliders permettent de faire varier les paramètres tels que le nombre d'unités et leur appropriation respective, le niveau d'exigence des unités et le rayon d'affectation. Nous constatons que si le rayon est de 1 cellule, il y a une concentration qui se fait. Tandis que si le rayon est plus élevé (3), une hétérogénéité se crée. Deuxième pas

A partir de cette première conclusion, nous avons décidé d'intégrer une troisième cellule unité représentant une industrie. Cette troisième cellule permet de créer une nouvelle condition qui vient perturber le système. Ainsi, une cellule d'habitation doit avoir dans un rayon r1, un nombre d'activités Y et aucune industrie pour être stable. A l'inverse, une industrie doit avoir dans un rayon r2 un nombre d'activités Y aucune habitations. Si les conditions ne sont pas satisfaites, le processus est réitéré jusqu'à ce que la condition soit satisfaite. 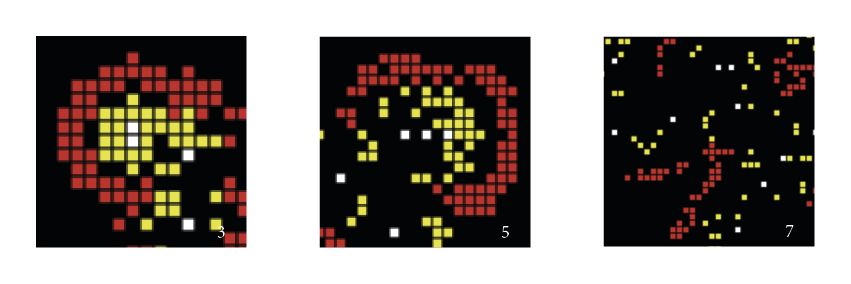Nous constatons ici qu'à travers ces nouveaux paramètres nous arrivons à la formation de pôles autour desquels gravitent les commerces et habitations. Si le rayon r2 de l'éloignement des industries par rapport aux habitations est faible, nous obtenons une structure similaire au modèle de Johann Heinrich von Thünen. Cette structure montre que des industries peuvent prendre un rôle essentiel dans la structure de certaines villes pour autant que les nuisances soient tolérées.

Au contraire, si l'exigence d'éloignement des industries par rapport aux habitations est élevée, les industries repoussent les unités d'habitations et nous avons une formations plus hétérogène, dépourvues de centralités. Toutefois de nos jours, nous tendons à avoir une plus grande mixité entre habitations et activités. C'est pourquoi nous avons décidé de rajouter une troisième condition où les commerces doivent avoir un nombre x d'habitants et un nombre Z d'industries dans un rayon r3 pour pouvoir être stable. Ainsi, il n'y a plus de ségrégations entre habitations et commerces et nous obtenons donc une plus grande mixité sociale. 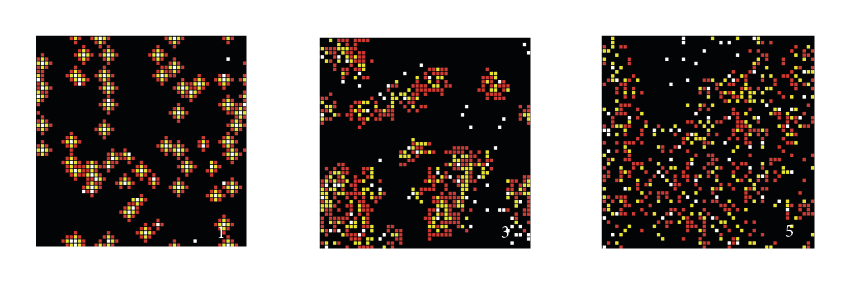Nous pouvons constater que plus le rayon d'affectation est faible, plus nous tendons à avoir une multitude de pôles d'attractions ayant pour centre une activité. Nous obtenons avec ce type de structure, un déplacement minime des habitants vers les commerces. Au contraire, si le rayon est élevé, une réelle mixité se crée entre habitations et commerces créant ainsi un tissage pouvant correspondre à une ville recherchant une mixité de fonctions. Toutefois, ces grands tissages impliquent un déplacement plus élevé des habitants vers les commerces. Cependant, dans un avenir proche, nous pourrions avoir des industries propres en complète harmonie avec le tissu urbain. Ainsi, il n'y aurait plus de phénomène de répulsion entre habitations et industries.

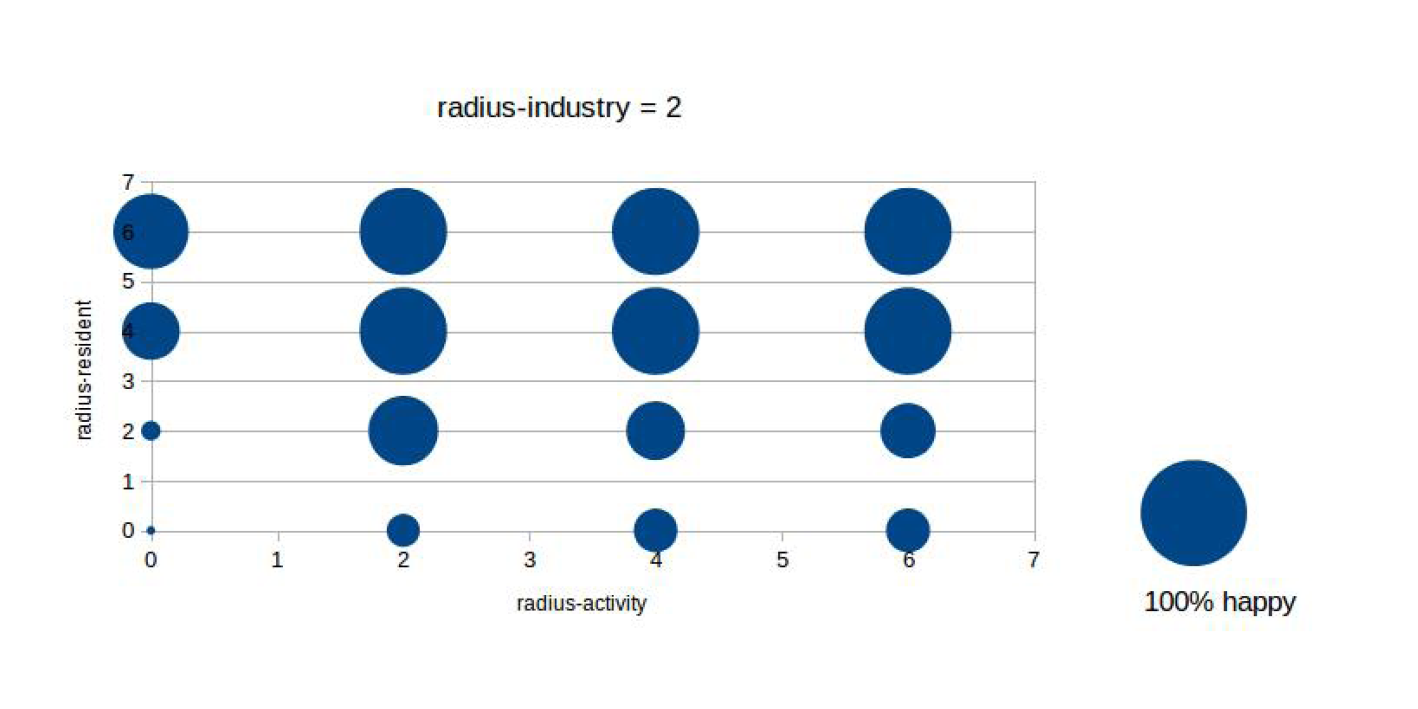
A nouveau, si le rayon d'affectation est faible, nous avons une multitude de pôles ayant comme noyau cette fois-ci les industries et les commerces. Au contraire, avec un rayon d'affectation plus élevé, nous avons une hétérogénéité totale avec une mixité complète entre habitations, commerces et industries. A travers le behavior space, nous avons voulu montrer au moyen d'un graphique l'influence du changement de radius des habitations et des commerces.

Nous pouvons constater qu'avec des exigences trop élevées, il est difficile de satisfaire toutes les conditions et une stabilité ne peut pas être trouvée. Au contraire, avec des exigences plus souples, nous avons une structure qui tend vers la stabilité. De plus, dû au rapport d'habitations plus élevé que les commerces, le rayon d'influence des habitations primes et la stabilité est fortement influencée par les conditions de celles-ci. Nous pouvons voir que les structures trouvées auparavant ont un degré de ségrégation et de compacité qui peut fortement évoluer en fonction de nos exigences.

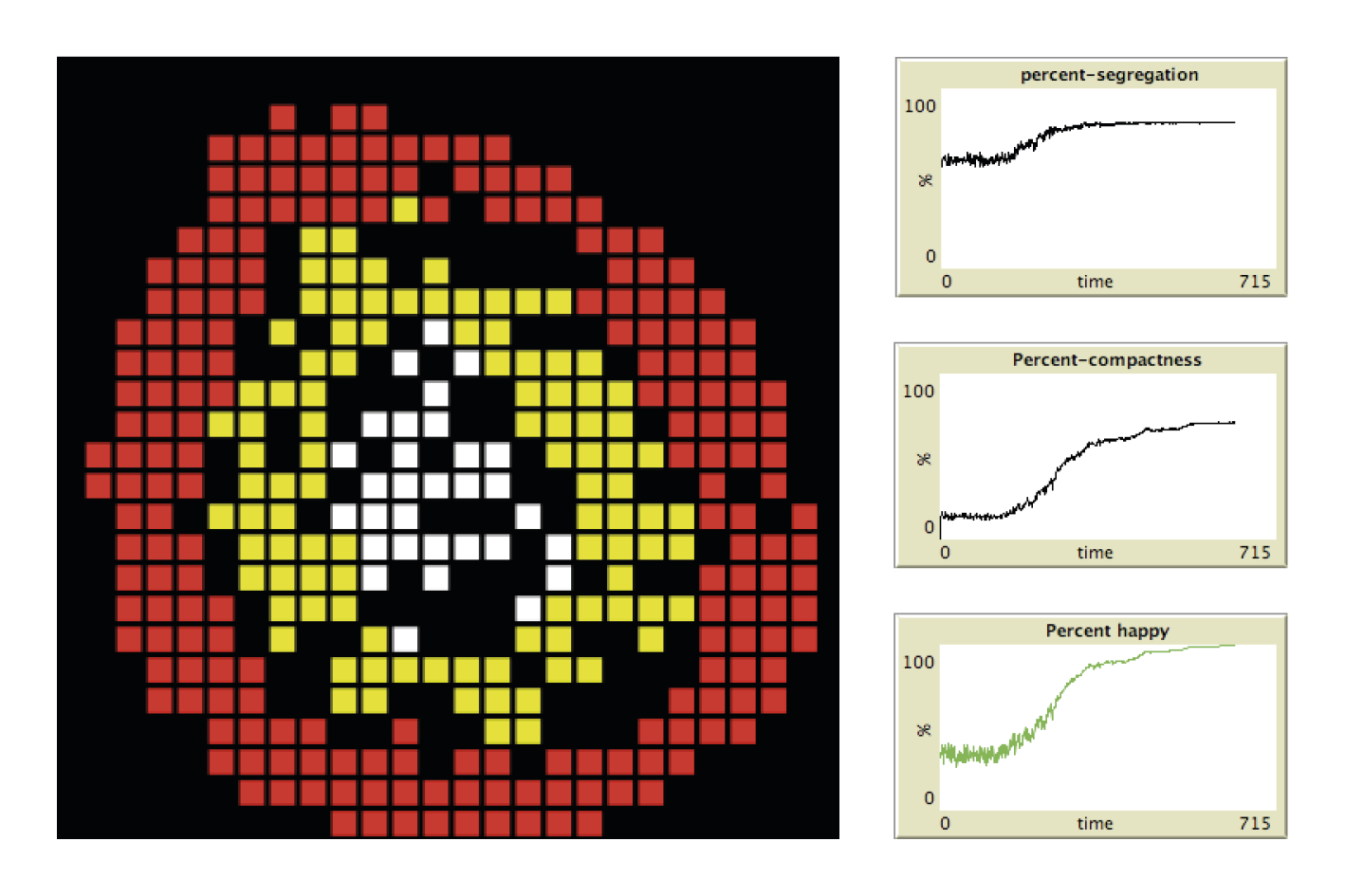
Ci-dessous, nous retrouvons la ville similaire au modèle de Johann Heinrich von Thünen, la ville du futur avec une mixité complète. Les tableaux nous indiquent leur taux de ségrégation, compacité et satisfaction respectifs. 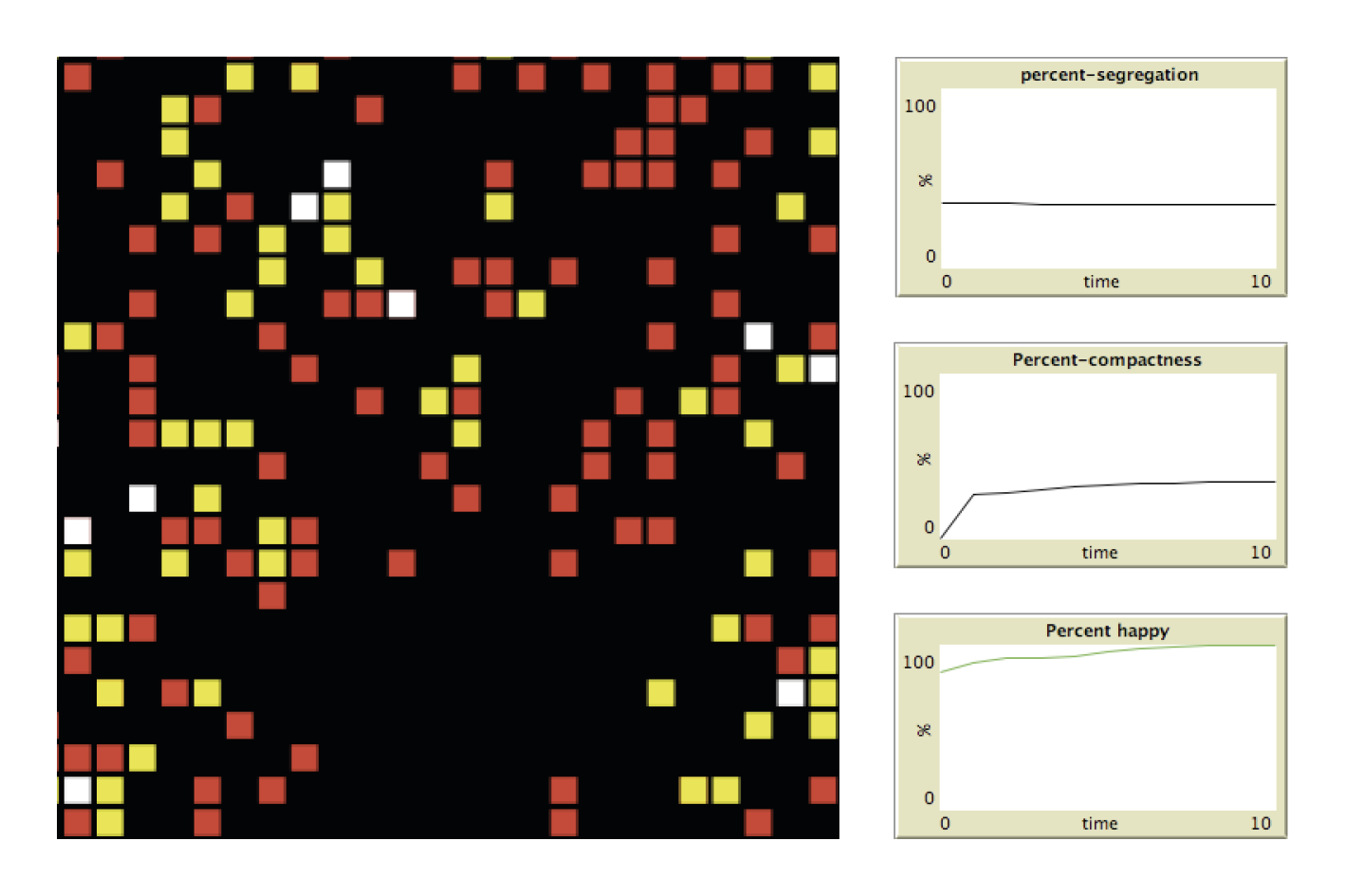Discussion et conclusion

A travers ce modèle fonctionnel, nous pouvons comprendre que le problème n'est pas simple. Nous avons émis l'hypothèse que nous pouvions résumer notre problématique à travers 3 types d'unités et leurs conditions respectives, mais la réalité est bien plus complexe. Divers autres facteurs viennent modifier ces structures tels que des facteurs sociaux, économiques, géographiques, temporels...

Toutefois, nous pouvons comprendre que dans un contexte neutre, ces relations sont cohérentes. Il est important de noter que plus les exigences sont élevées, plus le nombre d'itérations du processus est élevé (voir infini). Ainsi, trouver un équilibre avec un nombre d'exigence plus élevé est impossible et une question de temporalité s'impose.

Il serait intéressant d'ajouter selon les nécessités de nouvelles conditions et des nouveaux types unités. Ainsi, d'autres interactions pourraient être étudiées.