<<< EPFL Semaine ENAC - Modèles Basés-Agents

I. Introduction / Intérêt de la recherche

Le modèle que nous avons créé modélise la propagation d'un virus hydrique au sein d'une ville. Ce virus se répand dans les canalisations et infecte la population via la consommation des eaux infectées. A l'aide de cela, nous pouvons analyser l'influence de différents paramètres sur la durée de l'épidémie et les coûts pour l'éradiquer. Les paramètres que l'observateur peut modifier sont la taille de la ville, le niveau de traitement des eaux et les mesures prises pour immuniser la population.

Ce modèle est particulièrement intéressant du fait qu'il est concret et d'actualité. Il nous permet de vérifier l'effet, l'efficacité et le coût des mesures prises par la ville en question contre l'épidémie.

II. Objectifs et hypothèses

Nous avons pour objectif de trouver les mesures prises par la ville qui permettent de sauver la population, donc éradiquer l'épidémie, avec un coût minimum pour une ville de taille donnée.

En tant que première hypothèse, nous pensions que la taille de la ville influencerait les coûts pour éradiquer la maladie, c’est-à-dire qu'une grande ville aurait des coûts plus importants qu'une petite ville. Nous nous sommes aussi posé la question suivante: quel paramètre est le plus efficace pour éradiquer le virus ? Et quelle serait la combinaison de paramètres la plus efficace ? Et la plus rentable ?

III. Méthodes et procédures

Éléments

Fixes

Nous avons trois éléments fixes dans notre modèle.

• Le territoire, qui n'a aucune interaction avec les autres patches, est en vert, sert essentiellement de décoration pour l'interface graphique.

• L'eau se trouvant dans les canalisations est en bleu.

• La population peut se trouver en trois états différents: saine (patches noirs), contaminée (patches jaunes) et immunisée (patches blancs).

Mobiles

Les éléments mobiles sont les virus, qui se répandent aléatoirement dans l'eau, et sont représentés par des sputniks rouges.

Variables

Nous pouvons faire varier différents paramètres influençant la propagation du virus.

• D'une part, il est possible d'immuniser la population pour un certain temps. Il y a trois niveaux d'immunité, None, Water-bottles, Vaccines. Plus la prescription est sévère, plus vite la personne s'immunisera et plus longtemps aussi elle le restera. Le premier niveau représente l'immunité naturelle de la population. Le deuxième niveau représente la résistance de la population si on leur fournit des bouteilles d'eau, le contact avec de l'eau contenant des virus sera moindre mais pas nul et donc la personne risque d'être re-contaminée. Effectivement, bien qu'on ne boive plus de l'eau du robinet, on en fait toujours usage pour des raisons sanitaires (douches, etc.). Le dernier niveau indique la prescription de vaccins. La population vaccinée est immunisée et donc résistante au virus pendant un temps important. Par contre les virus subissent souvent des mutations donc la population au bout d'un certain temps redevient contaminable. Enfin, le temps d'immunité dépend de la mesure prise: il sera plus long pour une prescription de vaccins que pour une distribution de bouteilles d'eau.

• Ensuite, il est aussi possible d'agir sur la qualité de l'eau en y ajoutant un traitement. En augmentant le niveau de traitement, on diminue la durée de vie du virus.

De plus, un compteur enregistre les coûts de l'immunisation de la population et du traitement des eaux. Tandis que le prix des immunisations dépend du nombre de personnes infectées et du temps (car il y a mutation du virus), le traitement de l'eau consiste en une charge ponctuelle, car on suppose que les coûts majeurs sont dus à l'installation du traitement de l'eau, qui est unique.

Relations spatiales

Les agents sont donc les virus qui peuvent infecter la population et la rendre malade. Un virus se trouvant en relation avec une personne a 1 chance sur 10 (alpha = 0.1) de la rendre malade (noir->jaune). Une personne malade a 1 chance sur 100 (beta = 0.01) de produire un nouveau virus. Après un certain temps défini par le niveau d'immunisation, l'état des personnes passe de contaminé à immunisé (jaune->blanc).

Le compteur des coûts nous permet de voir s'il est plus avantageux d'investir dans une immunisation de la population ou dans un traitement des eaux suivant la taille de la ville.

Processus

Diagramme des flux

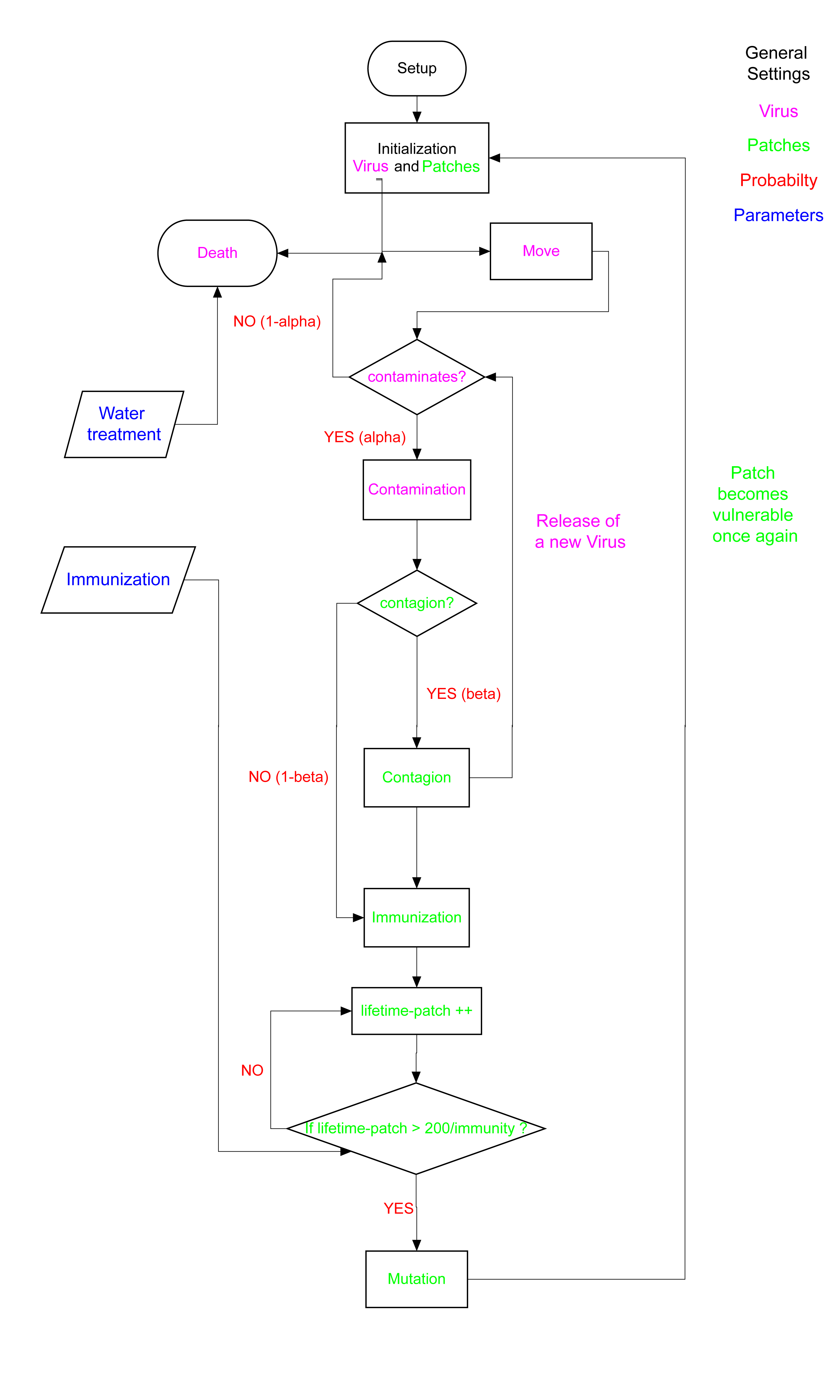
IV. Résultats

Observations globales du comportement

Propagation du virus

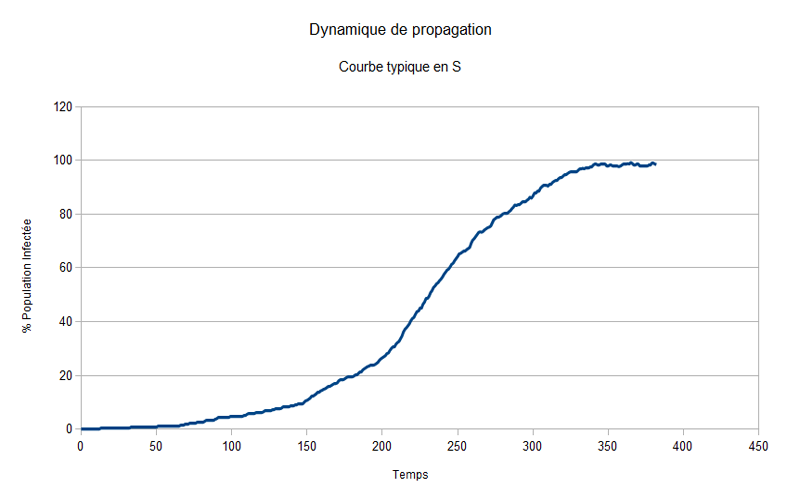
On observe que si l'on ne fait rien pour réduire le virus, le graphe de l'infection de la population suit la forme typique d'une épidémie, un S, montrant ainsi qu'elle a une phase de latence, une phase exponentielle et une phase de saturation.

Cela s'explique très simplement: au début, le nombre de virus est plus faible donc l'infection est lente et la pente est faible.

Par la suite, le nombre de virus augmente impliquant ainsi une infection rapide de la population et la pente du graphe augmente.

Et finalement, une fois que le pourcentage de la population infectée est fort, il sera plus difficile pour un virus d'infecter une personne saine et donc l'infection sera plus lente et la pente plus faible.

Analyse

Effets du traitement de l'eau sur la propagation du virus

A chaque fois que l'on monte d'un niveau le traitement de l'eau, le pourcentage de la population malade descend d'environ 20%.

Effets de l'immunité sur la propagation du virus

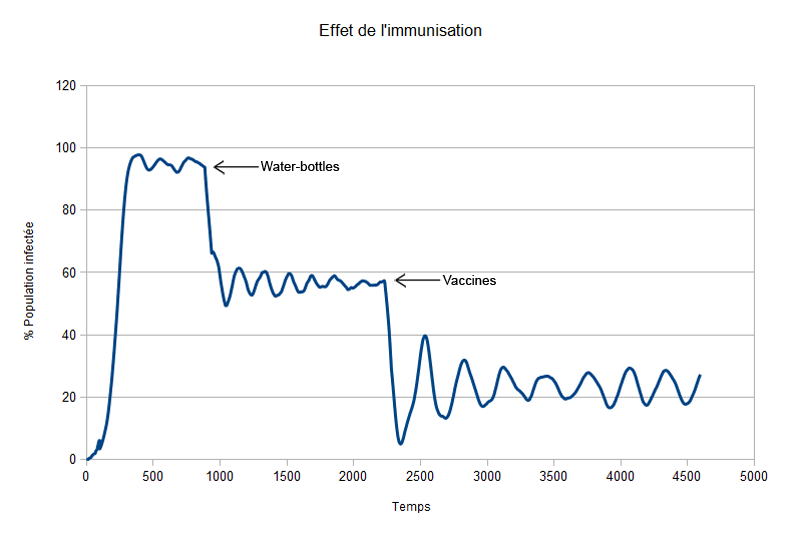
L'immunisation de la population fait baisser à chaque intervention le pourcentage de personnes malade de 40%.

Effet combiné du traitement et de l'immunité sur la propagation du virus

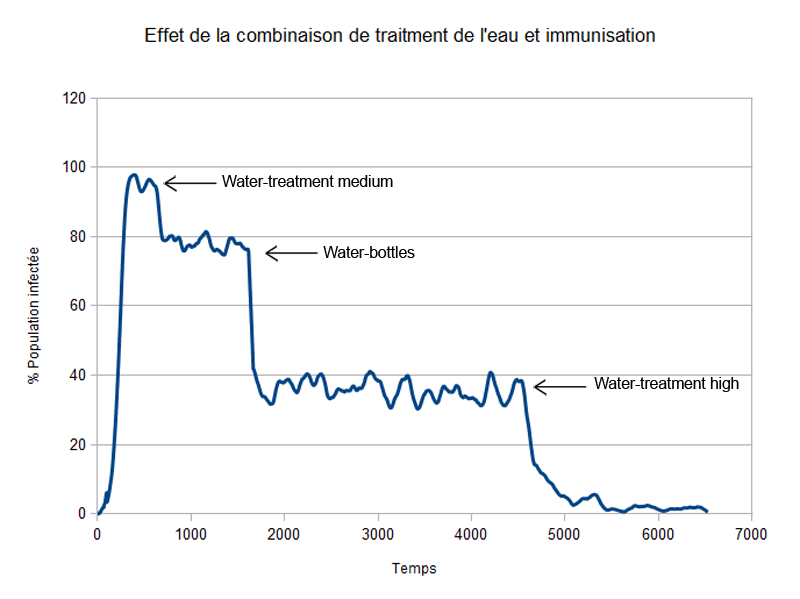
On observe qu'un seul traitement isolé, aussi fort soit-il, que ce soit un traitement de l'eau ou une immunisation de la population ne suffit pas à éradiquer la maladie, tandis qu'une combinaison des deux permet de sauver la population avec grande efficacité.

Effet des paramètres par rapport aux coûts

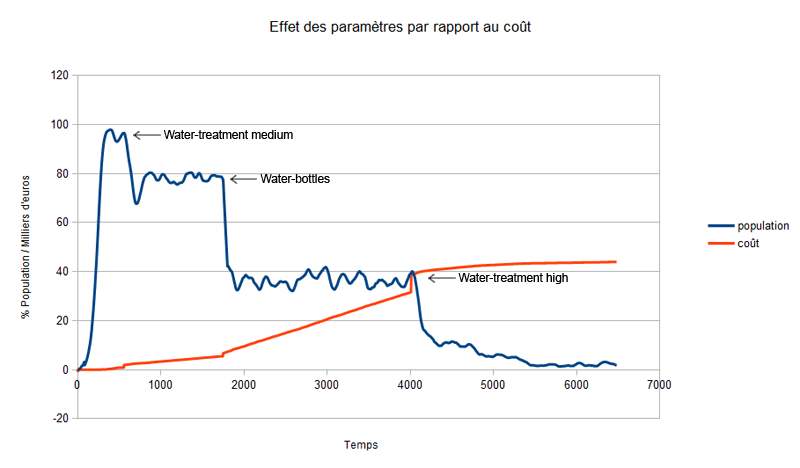
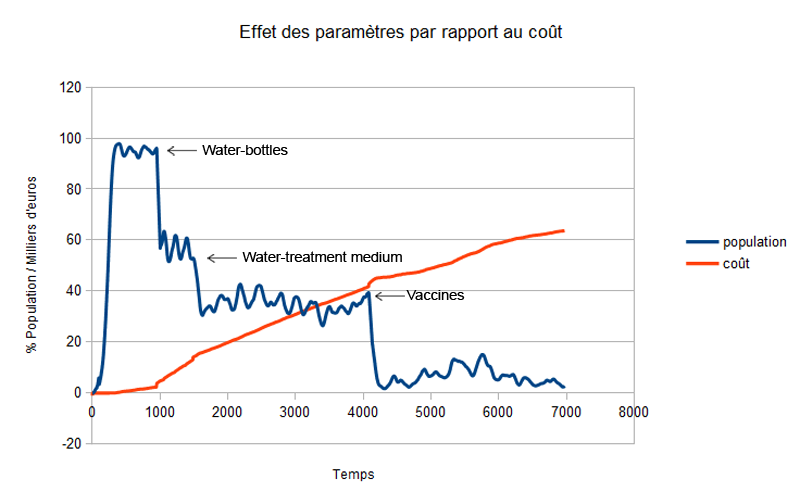
Nous observons que pour éradiquer la maladie, les coûts changent par rapport à la combinaison de traitements utilisés par la ville. En effet la solution la plus rentable pour la ville consiste à traiter l'eau et distribuer des bouteilles à la population , en éradiquant ainsi la maladie sans avoir recours aux vaccins.

Efficacité des paramètres

Ces diagrammes obtenus à l'aide d'un behaviour-space nous montrent l'effet combiné des paramètres sur la virulence du virus, et donc le pourcentage de population infectée pour une certaine taille de ville.

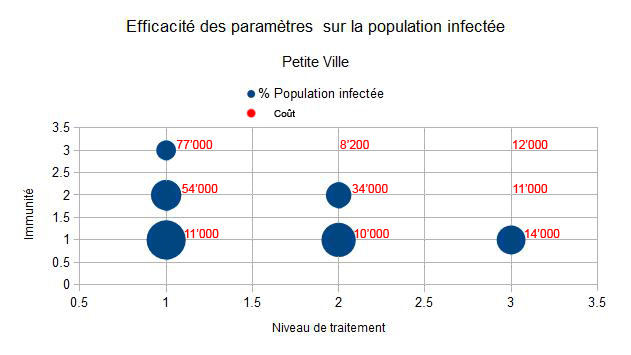
Pour une petite ville on peut voir qu'il est plus avantageux, en terme de coût, de mettre un traitement de l'eau moyen (2) et une immunité avec vaccins (3) pour éradiquer le virus.

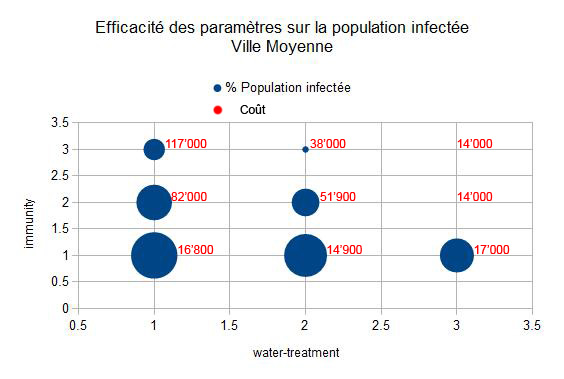
Une ville moyenne aurait avantage a mettre un fort traitement des eaux (3) combiné à une immunité par accès à des bouteilles d'eau (2).

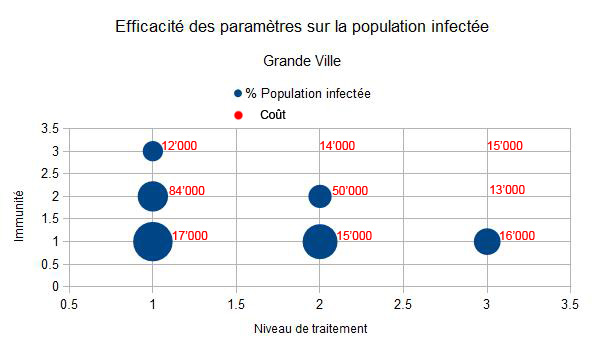
Et enfin, pour une grande ville, il est avantageux de faire comme pour une ville moyenne.

Si les paramètres ne permettent pas d'éradiquer le virus, les coûts vont toujours augmenter car ils dépendent du temps. On constate donc que la meilleure solution est de contrer l'épidémie avec un grand effort au début plutôt que de traiter légèrement pendant une longue durée, sans jamais venir à bout du virus.

V. Discussion et conclusion

En conclusion, contrairement à ce que nous pensions, la taille de la ville n'a qu'une influence minime sur la propagation du virus. Le coût pour la ville augmente avec la taille de la ville mais ceci n'est pas représentatif car une grande ville a plus d'habitants et donc plus de revenus fiscaux. Nous avons donc calculé le coût par habitant et nous observons que celui-ci ne change pas par rapport aux trois tailles de ville que nous testons dans notre modèle. Nous pouvons en revanche constater que seules deux combinaisons de nos paramètres, immunité et traitement, permettent une disparition totale du virus. Nous avons également observé que suivant la combinaison choisie de nos paramètres, le coût total varie radicalement. En outre, ce modèle prouve qu'il faut privilégier une mesure forte et drastique dès les débuts de la propagation de la maladie plutôt que d'effectuer un traitement léger, qui durerait longtemps et deviendrait coûteux, mais qui ne pourrait jamais éradiquer définitivement l'épidémie.

Proposition de développement

Si nous avions la possibilité de continuer notre modèle, nous pourrions choisir d'injecter les traitements et les immunités par secteur, donc par exemple mettre en quarantaine ou prescrire des vaccins seulement à la zone contaminée, comme il advient en réalité. Nous pourrions aussi imaginer un nouvel état à nos patches population. En y ajoutant l'état de mort, nous pourrions voir avec quels paramètres, la ville tendra à disparaître ou à guérir. Qui survivra ? l'homme ou le virus ?