<<< EPFL Semaine ENAC - Modèles Basés-Agents

Résumé

• Le travail produit modélise le déplacement des rames de métro sur la ligne M1 (Lausanne).
• L'objectif est d'influencer les paramètres fréquence d'injection des rames, vitesse, temps d'attente à chaque station et le nombre de rames présentes sur la ligne pour trouver une configuration où les retards et conflits (trop de métros à une station) sont minimaux.
• Les agents sont les rames et les patchs les voies et stations.

Introduction / Intérêt de la recherche

Le trafic ferroviaire est en général pensé et modélisé de façon top-down. Peut-on le modéliser suivant un processus bottom-up, et comment ? (C'est-à-dire, le trafic peut-il être défini en fonction des paramètres des rames elles-mêmes?)

Objectifs et hypothèses

• Objectifs : Modéliser un trafic ferroviaire (métro) de type bottom-up selon des paramètres de fréquence d'injection, vitesse, temps d'arrêt, nombre de rames en circulation.
• But : parvenir a une configuration optimale d'un maximum de deux métros arrêtés par station (voire un seul métro pour certaines stations – Bassenges p.ex)avec un minimum de retard en cirulation.
• Hypothèse : avec un temps d'arrêt minimal à chaque station et une information en temps réel, une fréquence optimale peut être trouvée pour une certaine vitesse de circulation des rames.
  • Les premiers tests seront réalisés avec une possibilité de croisement des rames à chaque station.
  • Les test suivants sont réalisés avec une modélisation plus réaliste : les stations Provence, Sorge et Bassenges ne permettant plus le croisement de deux rames (comme c'est le cas pour le m1).
    

Méthodes et procédures

On modélise le m1.

• Éléments
  • Fixes : Quatre types de patchs sont crées : dépôt, stations, rails, terminus.
  • Mobiles : Les agents (turtles) sont les rames de métro, se déplaçant sur les patchs rails et stations.
• Relations spatiales : Un patch représente 50m tandis que un tick est considéré comme 1s. Chaque type de patch a ses propriétés, et patchs et agents interagissent.
  • Les patchs rails ne peuvent accueillir qu'un seul agent à la fois, peu importe sa direction.
  • Les patchs stations imposent l'arrêt aux agents et peuvent accueillir un nombre (pour l'instant !) illimité d'agents.
  • Les patchs terminus sont des stations aux extrémités de l'espace, qui imposent aux agents de faire demi-tour afin de poursuivre leur trajet dans l'autre sens.
  • Le patch dépôt est situé à "EPFL". Il représente le lieu d'injection des rames de métro sur le parcours.
  • Les agents ont le pouvoir de changer l'état du patch rail de « libre » à « occupé ».
  • Un agent ne peut quitter une station que si le patch rail sur lequel il veut se rendre est libre.

Processus

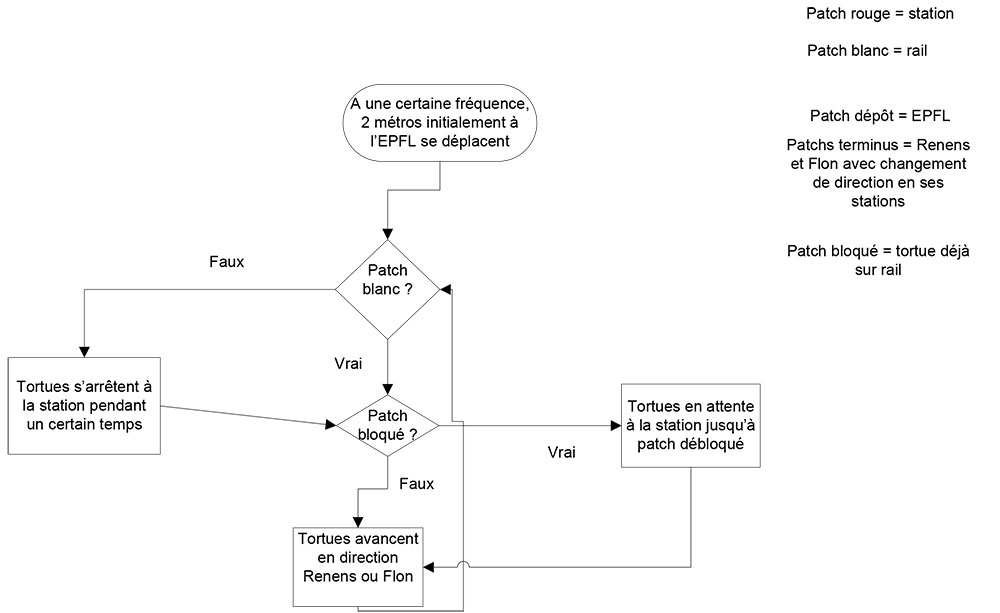
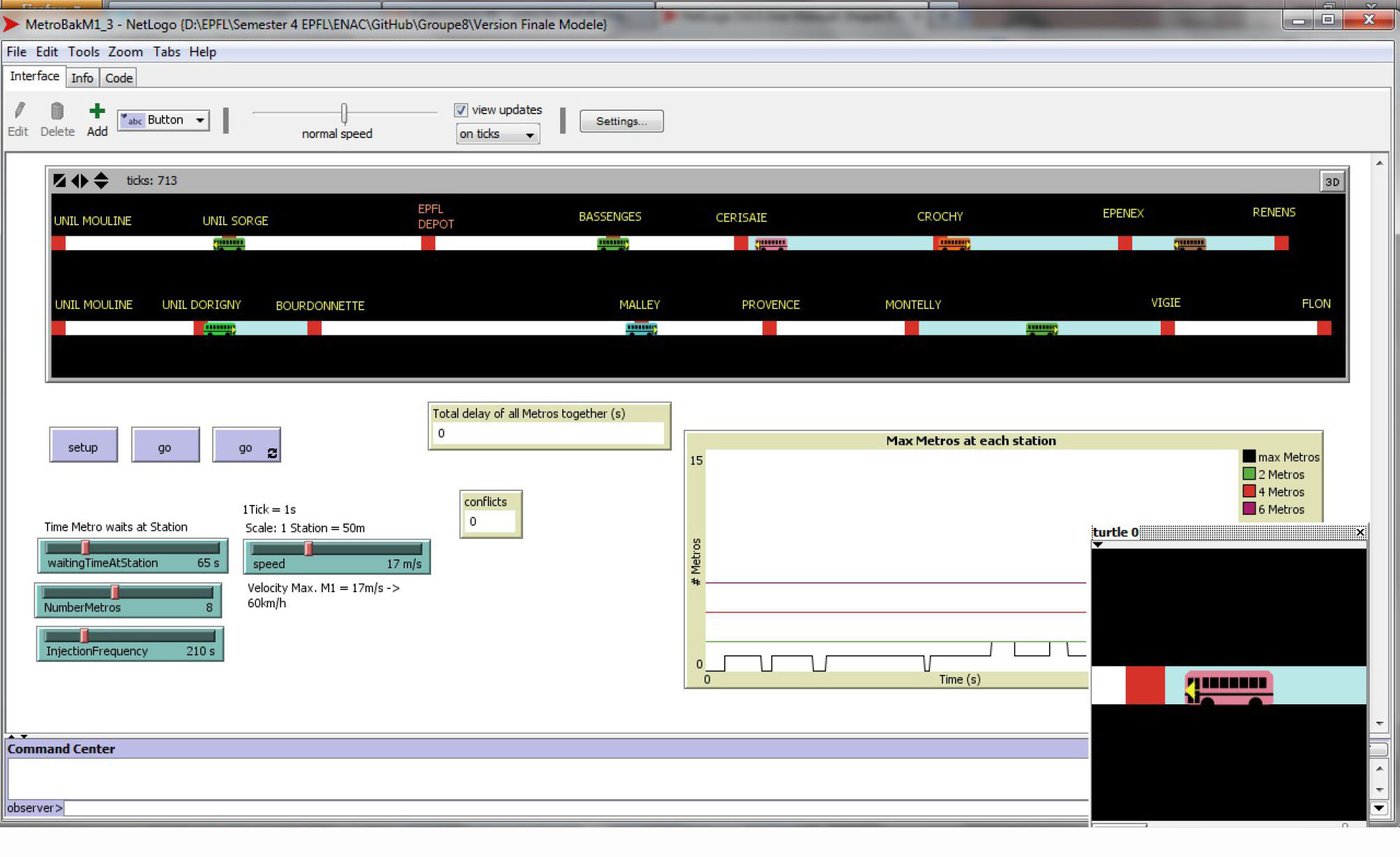
Résultats

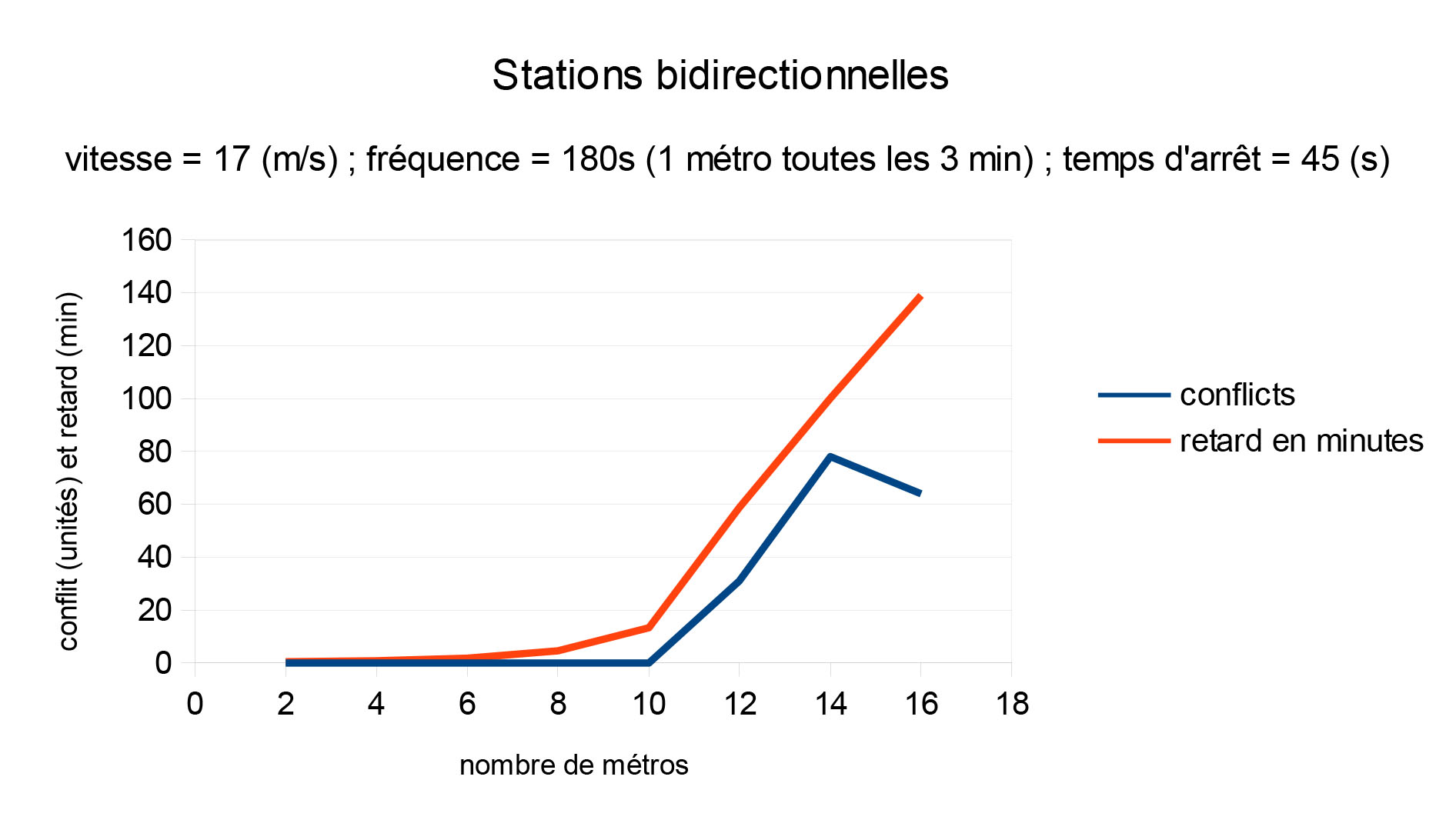
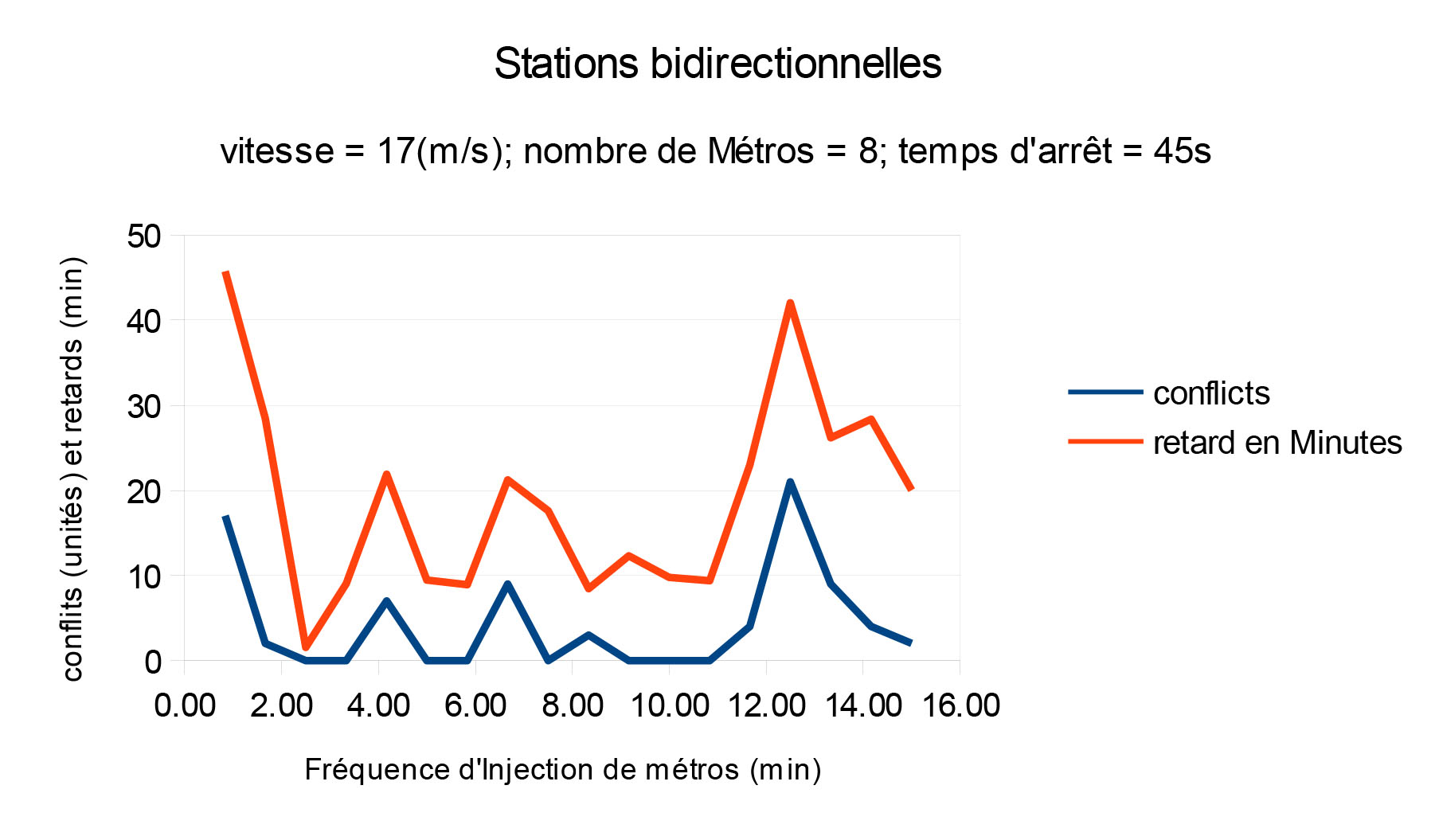
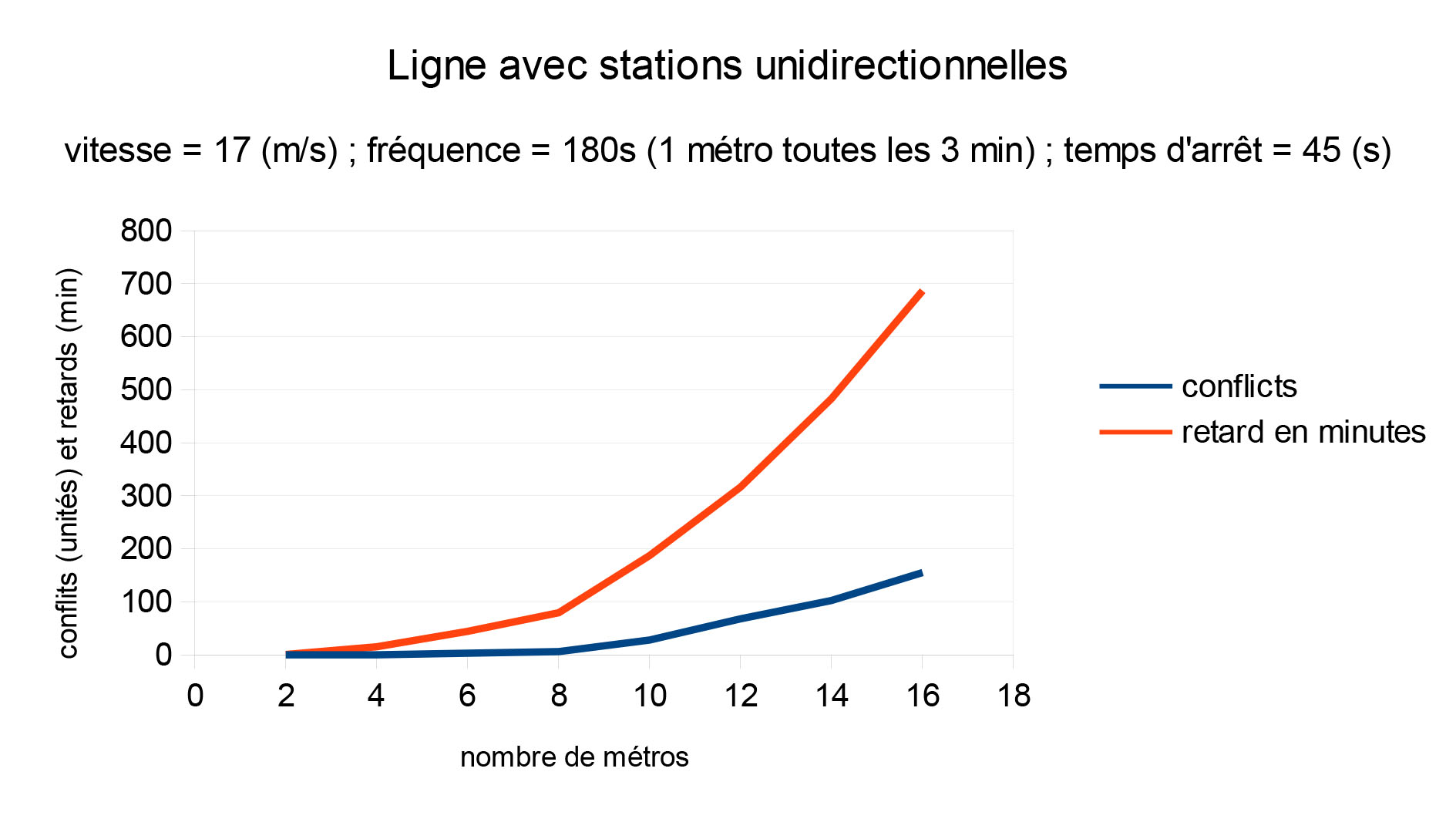
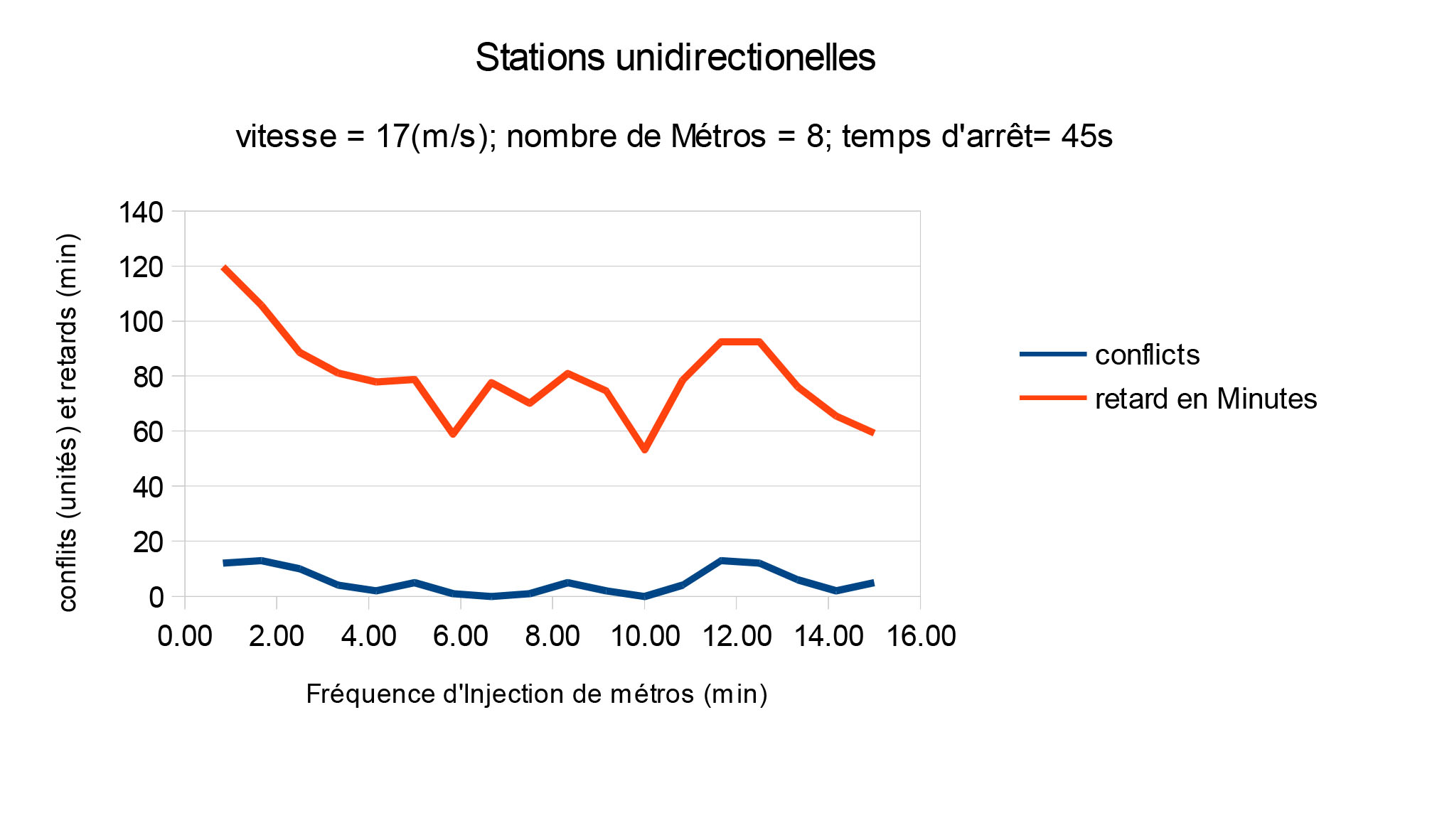
Pour obtenir ces résultats, nous avons fixé deux paramètres (en effet, pour n'avoir qu'une variable en abscisse !) : la vitesse des rames est de 17m/s, le temps d'attente en station est de 45s. (On considère que les rames vont au maximum de leur vitesse et que le temps d'attente est minimal). Les variables pour tester conflits et retard sont alors la fréquence d'injection des métros et le nombre de métros en circulation.

Bien que les deux modèles testés diffèrent (l'un ne possède que des stations ou les métros peuvent se croiser, l'autre possède 3 stations où le croisement est impossible),les graphes produits présent des allures similaires :

• En faisant varier le paramètre de fréquence d'injection des métros, on remarque que

  • Pour la ligne où le croisement est possible à toutes les stations, le retard max avoisine 45 minutes.
  • Pour la ligne où le croisement est impossible à 3 des stations, le retard max avoisine 120 minutes.
    • -> La ligne avec des stations unidirectionnelles semble donc être moins performante au niveau des retards.
  • Cependant, la variation des conflits reste sensiblement similaire dans les deux cas.
  • Les deux graphes présentent un aspect en dents de scie.

• Lorsque c'est le nombre de métros qui varie, on remarque sans surprise que moins il y a de métros, moins il y a de retards ou conflits. Cependant :

  • Pour le modèle où le croisement est impossible à 3 stations, l'augmentation du nombre de métros semble faire croître indéfiniment le nombre de conflits et de retards, malgré une première phase plutôt satisfaisante.
  • Pour l'autre modèle, un pic des conflits a lieu lorsque 14 métros circulent, mais au-delà les conflits diminuent -> Le modèle semble tendre vers une régularisation, ou un cycle. Là aussi, les retard augmentent avec le nombre de métros. Une fois de plus, la ligne permettant le croisement à toutes les stations présente de meilleures performances.

Discussion et conclusion

• Conclusion
  • Ce modèle nous a permis de modéliser un trafic ferroviaire de façon bottom-up, pour que les agents règlent eux-même leur circulation en transmettant des informations aux patchs sur lesquels ils circulent.
  • Avec les paramètres choisis - 17m/s et 45s de waiting time. Le parcours d'un métro sans retard est de 19min (1140ticks). Sur la durée des 8000 ticks que tourne le modèle, un metro peut faire en principe 7 tours du système.
  • On remarque que le modèle le plus efficace, avec lequel on parvient à n'avoir aucun conflit ni retard, est celui où le croisement est possible à toutes les stations. Dès que l'on insère les stations unidirectionnelles (telles que dans la réalité...) le modèle est nettement moins performant !
• Application
  • Ce modèle pourrait être utilisé pour des rames "intelligentes" qui n'interagiraient qu'entre elles et dont la coordination ne dépendrait pas d'un contrôle supervisé.
• Pour poursuivre
  • En ajoutant les passages à niveaux (croisement des rails avec le trafic routier), le modèle serait encore plus complet, introduisant de nouveaux temps d'attente en station.
  • Il serait intéressant de programmer des tronçons à deux rails, pour les que les rames puissent se croiser en circulation, puis d'étendre ce concept à toute la ligne : ainsi, on réduirait les conflits puisque le croisement serait aussi possible hors des stations.
  • Un "waiting-time" stochastique pourrait modéliser d'éventuels problèmes retardant le départ de la station (accident, porte coincée...)
  • Réussir à programmer la sortie de certains métros afin de modéliser des fréquences différentes tout au long de la journée (plus de métro à midi qu'à 15h00 par exemple) pourrait nous permettre de tester si le retard est rattrapable.
  • Pour aller encore plus loin, modéliser de nouveaux agents qui seraient les passagers afin d'observer le flux de voyageurs, et ainsi introduire une variable stochastique.